前章で3次関数のグラフを考えた。
そのときは、
①導関数を求める。(微分する)
②求めた導関数から増減表を作る
③x切片、y切片、極値などを調べて、グラフを書く
そ3手順で書いた。
しかし、高次関数になると、求めるのが大変になりすぎる。
そこで、大局的考察と局所的考察をして、グラフの概形を推定することを試みる。
=大局的考察=
f(x)=aₙxⁿ+aₙ₋₁xⁿ⁻¹+……+a₁x+a₀
というn次関数を考える。
このとき、最高次係数aₙの符号とnの偶奇によって、以下の4つのパターンに分類できる。
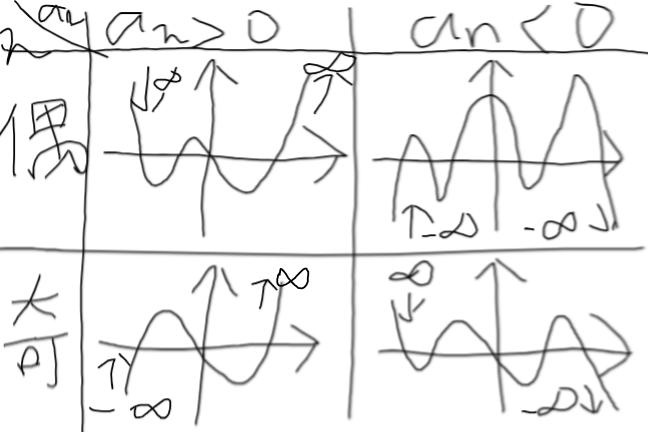
=局所的考察=
n次関数が(x-α)^kを因数に持つとき、kによって、(α,0)周辺での挙動が特徴的になる。
k=1のとき
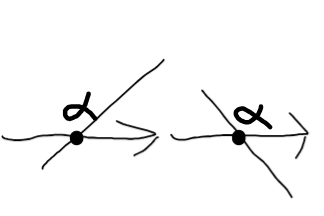
kが偶数のとき
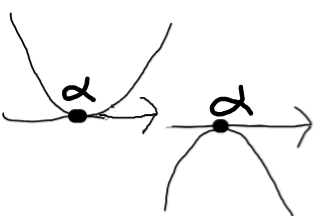
kが3以上の奇数のとき
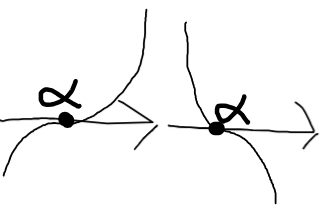
さらに、因数分解された形から増減表を上手に書き、グラフを推測することもできる。
偶関数……f(-x)=f(x) y軸に関して対称
f(x)=x²、f(x)=cos x etc.
奇関数……f(-x)=-f(x) 原点に関して対称
f(x)=x³、f(x)=sin x etc.
最大値・最小値も増減表をうまく利用する。