「東進数学特待日記」シリーズでは、数学特待生として東進の数学の授業を受けた感想を書いている。
数学特待制度についてはこちらの記事を見てほしい。
※あくまで、メモである。(見やすくは作っていない)
第5章の不等式と極限では、「不定形の極限」という概念を学習した。
不定形の極限とは、ぱっと見では収束するか発散するかがわからない極限のことである。
(0/0)型と呼ばれる、分母と分子がともに0に近づく極限、
(∞/∞)型と呼ばれる、分母と分子がともに∞に近づく極限、
(∞-∞)型と呼ばれる、引く数と引かれる数がともに0に近づく極限、
(0×∞)型と呼ばれる、0に近づく数と無限に近づく数の積の極限、
(0^0)型と呼ばれる、0に近づく数を0に近づく数乗する極限、
(1^∞)型と呼ばれる、1に近づく数を無限に近づく数乗する極限、
(∞^0)型と呼ばれる、無限に近づく数を0に近づく数乗する極限、
がある。
不定形の極限を計算するには、
・式変形で不定形を解除する
・「はさみうちの定理」を用いる
という手法がある。
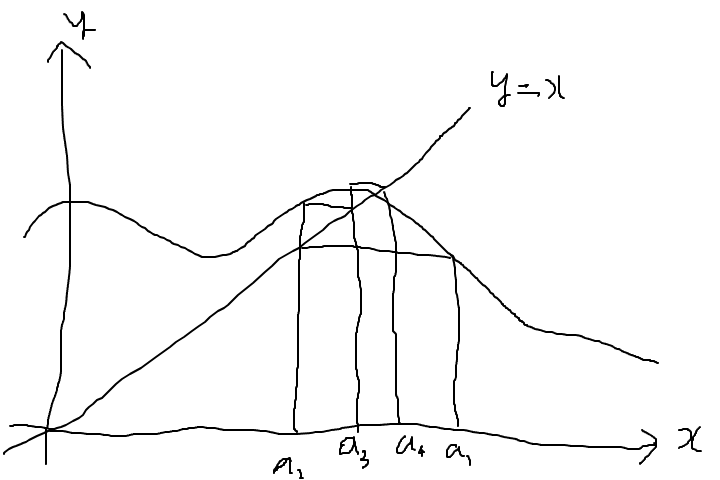
第6章の数列の極限では、関数のグラフ上の1ずつ増えていく点を考えて、収束や発散を求めた。
また、y=f(x)のグラフを描いて、そこにy=xの線を入れて、
数列の1項をx軸上にとって、グラフにあたるまで上に伸ばす。
グラフにあたったら、同じy座標のy=x上の点まで伸ばす。
そこから真下に伸ばし、x軸にぶつかったところが2項である。
同様に繰り返していくと視覚的に数列の極限がわかる。